La naturaleza está llena de fantásticos enigmas y maravillosas composiciones que escapan a nuestra comprensión: árboles, flores, vegetales, y hasta nuestros propios pulmones, están configurados siguiendo un orden, unas normas en su formación que perfilan un equilibrio mágico que nos sorprende y nos inquieta. Los fractales forman parte de nuestra biología y nuestro arte, también de nuestras matemáticas, un reto de la geometría que seguro te encantará conocer.
La naturaleza de los fractales
Los fractales son objetos que se repiten, tienen autosimilitud y son recursivos unos con otros. Dicho de forma más sencilla: si cogemos un trocito de un fractal nos daremos cuenta que es igual a la figura principal. Pero pongamos un ejemplo: un abeto. Si arrancamos una de sus ramas y la observamos nos daremos cuenta de que ese pedazo que hemos cogido tiene la misma forma que el árbol completo. Otro más… cojamos ahora un brócoli de nuestra nevera para estudiarlo unos segundos, enseguida te darás cuenta que cada una de sus pequeñas partes es idéntica a la forma principal, es decir las partes más pequeñas que lo conforman, son igual al objeto que lo contiene. ¿Curioso, verdad?
Otro aspecto interesante sobre los fractales es que son fraccionarios, es decir no son unidimensionales, bidimensionales o tridimensionales, como son la mayoría de las cosas que nos rodean, en absoluto, no se pueden expresar por números enteros, de ahí que se les llame «fractales», porque son fracciones de un mismo objeto. Ejemplos que la biología y la naturaleza nos deja sobre los fractales pueden ser las esponjas de mar, el caparazón de un caracol, las hojas de los árboles, los tentáculos de los pulpos, el pulmón humano, los capilares…
Fractales en la geometría
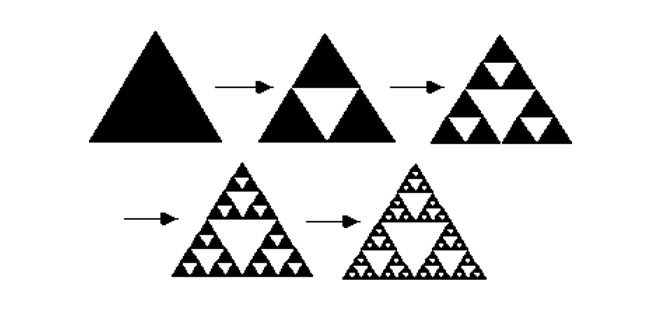
Las aplicaciones matemáticas y geométricas de los fractales son infinitas, y una muestra de ello sería por ejemplo el triángulo de Sierpinski, una figura inventada por el matemático polaco Waclaw Sierpinski en 1915. Seguro que hasta tú mismo has realizado estos juegos alguna vez, se empieza con un triángulo equilátero, después, en su interior dibujamos otro triángulo, cuyas esquinas, deben coincidir con los puntos medios de cada lado del triángulo mayor (quedará como una figura invertida). Ahora seguimos dibujando triángulos en cada esquina, hasta que poco a poco veremos como nos va quedando una figura habitada por miles de pequeños triángulos… este es un ejemplo muy sencillo de fractales en geometría, luego, tenemos conceptos más complicados pero a su vez más hermosos, como son por ejemplo los llamados conjuntos de Julia, donde se representan figuras a través de los llamados algoritmos de tiempo de escape, donde cada pixel de las figuras se colorean según el número de interaciones necesarias para escapar.
Puede resultar algo complejo, pero el resultado de estas formulaciones nos dejan auténticas bellezas para las cuales no hace falta la comprensión… y es que, en ocasiones, pensamos que la naturaleza está regida por el caos y lo imprevisible, pero en cierto modo, lo que nos rodea, e incluso lo que somos, responde a un orden específico, y los fractales es un mágico ejemplo de ello.